科学探索|15年磨一剑：张益唐证明黎曼猜想相关问题？11月论文见( 三 ) 15年磨一剑：张益唐证明黎曼猜

文章图片

对此，“科學大抖宅”正巧在一篇文章中对此做了非常白话的解释。
我们都知道，2、3、5、7、11这些数，除了1跟自己本身以外，不能被其他正整数整除，因此它们被称作质数。而所有大于1的正整数，都能够以质数的乘积来表示。
但如果要问：“比某个特定数值要小的质数有多少个呢？质数在整个数列中的分布情况又是如何？”
这个问题就复杂了。
而黎曼发现，质数的分布跟某个函数有着密切关系：

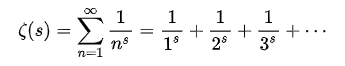
文章图片

这个公式中，s是复数，可以写成s=a+bi这样的形式（a是s的实部、b是s的虚部、i则是根号负一）。
数学家们可以轻易证明，只要s的实部大于1，那么整个无穷级数里，把每一项的绝对值相加后，会得到收敛并趋近于某个定值的结果。
不过，对于s的实部小于1的状况，事情就没那么简单了：整个级数和可能会发散。
但我们又想要扩充函数的定义，让它适用更广泛的范围，那该怎么办呢？
只需运用一些“简单的”数学技巧，就可以把上面的黎曼ζ函数改写为：

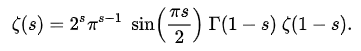
文章图片

其中的 Г ，称为伽玛函数（gamma function）。
由此可以发现，当s为负偶数（s= -2, -4, -6…）时，黎曼ζ函数为零。这些s的值，就称为平凡零点。
但是，除了平凡零点之外，还有其他一些s的值，能够让黎曼ζ函数为零──称为非平凡零点；它们不但对质数的分布有着决定性影响，实数部分还全都位于零和一之间。
到了这一步，已经到达了黎曼本人也无法证明的难度了。
不过他做了一个猜测，这些非平凡零点有着共同的特性：黎曼ζ函数所有非平凡零点的实部都是二分之一。
这就是赫赫有名的黎曼猜想。
孪生素数猜想
最后，让我们看看曾让张益唐名声大震的“孪生质数猜想”相关论文。
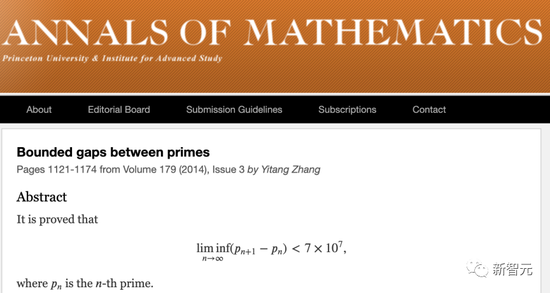
1992年博士毕业于普渡大学，张益唐度过一段坎坷的时光，终于在2013年，他对于“存在无穷多个差值小于7000万的质数对”的证明在五周内被《数学年刊》接收。

文章图片

论文地址：https://annals.math.princeton.edu/2014/179-3/p07
在这篇论文中，他找到了孪生素数对差值的上界——7000万，这是“孪生质数猜想”的重大进展，实现了从0到1的跨越。
后来，陶哲轩等数学家迅速将这个差距缩小到了246，但这相当于从1到2的跨越。相较而言，张益唐从0到1的这一步，意义更加重大。
关于两位数学家的研究成果，已经被拍成纪录片。

文章图片

根据《光明日报》采访人员王庆环的整理，在2016年度的“求是奖颁奖典礼”上，著名科学家杨振宁曾用小学生听得懂的语言讲解了张益唐所做的研究——

文章图片

文章图片

文章图片

对于以上解释，张益唐本人表示：“杨振宁教授的介绍既通俗又清楚，如果让我自己讲的话，我肯定讲不了那么好。”