外接球半径万能公式是什么
【外接球半径万能公式是什么】外接球半径万能公式:R=√[R_1^2+R_2^2- (L^2)/4] 。 若相互垂直的两凸多边形的外接圆半径分别为R_1 , R_2 , 两外接圆公共弦长为L , 则由两凸多边形顶点连接而成的几何体的外接球半径 。
文章插图
方法:
设A-BCD是正三棱锥 , 侧棱长为a , 底面边长为b ,
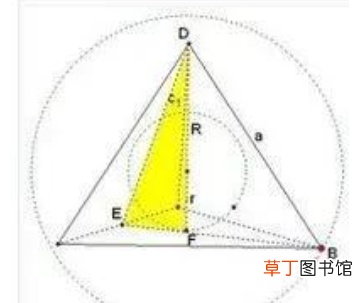
则外接球的球心一定在这个三棱锥的高上 。 设高为AM , 连接DM交BC于E , 连接AE , 然后在面ADE内做侧棱AD的垂直平分线交三棱锥的高AM于O , 则0就是外接球的球心 , AO , DO是外接球的半径 。
设AO=DO=R 。
则 , DM=2/3DE=2/3*2分之根号3倍的b=b/根号3 。
AM=根号(a^2-b^2/3) 。
OM=AM-A0=根号(a^2-b^2/3)-R 。
由DO^2=OM^2+DM^2得:R=根号3倍的a^2÷2倍的根号(3a^2-b^2) 。
无相关信息
推荐阅读
- 北方有这么一种早点——卷饼,卷饼可是万能的
- 【方法】如何自制万能杀虫水 方法是什么
- 平安智慧星少儿万能险怎样反还钱
- 【嫁接】什么树是万能嫁接树
- 万能香辣酱,一点儿不夸张
- 夏天吃烧烤,教你自制“万能蒜蓉酱”,烤茄子、花甲统统管用!
- 手机知识|手机验钞机软件哪个好,万能验钞机下载
- 【烂根】万能浇水神器,就是1根小吸管,专治烂根黄叶
- 手机知识|哪个app能遥控电动门,电动伸缩门手机遥控器万能
- 【花】养花万能水,竟是它!绿叶促花杀虫,样样行

















